Rate of Return
1. What Is a Rate of Return
A rate of return, or a return, is the cumulative P/L of your investment over a specific time period, expressed as a percentage of your initial cost. You can use it to measure the performance of your investment over time. Please note that if you make frequent or large transfers of funds or stocks to or out of your account during the period, you may get different rates of return by using different calculation methods. Therefore, it is very important to choose the appropriate method. There are many ways to calculate the rate of return, but each has its own advantages and disadvantages. Based on industry practice and having considered its own business characteristics, FUTU APP calculates your rate of return by using the following three methods: simple Dietz method, money-weighted return method (modified Dietz method), and time-weighted return method (TMR).
2. Calculation Methods for Rate of Return
2.1 Simple Dietz Method
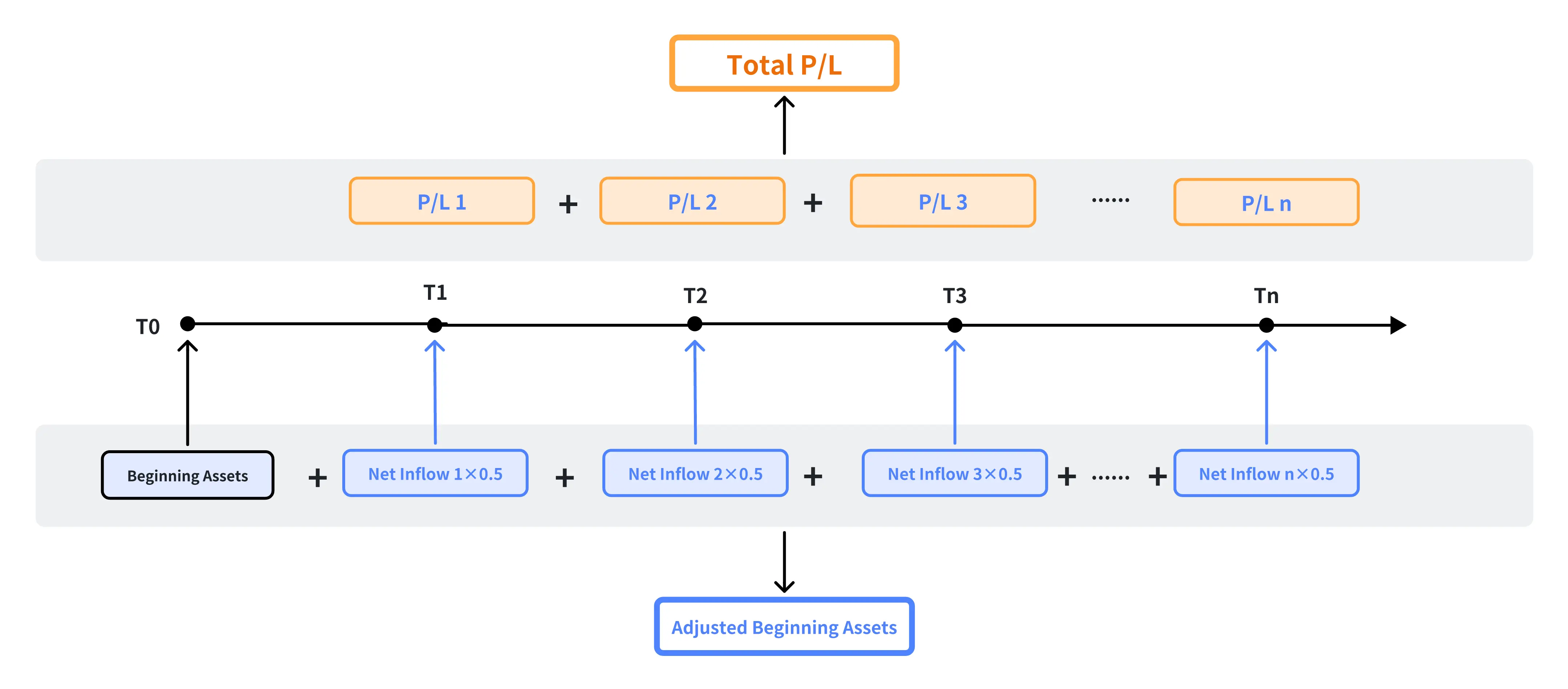
Assuming that all funds or stock transfers (hereinafter referred to as "net inflows") come from the middle of the period, this method calculates the impact of these net inflows by using a coefficient of 0.5 and thus gets the adjusted beginning assets. In general, this method is simple, easy to understand, and may be more appropriate for accounts with less frequent or smaller deposits and withdrawals.
Formula: Total Rate of Return = Total P/L / Adjusted Beginning Assets
Example:
| Date | Net Inflow | Daily P/L | Total Assets | Calculation |
| January 2, 2023 (beginning of the period) | -- | -- | 100,000.00 | Total Rate of Return = 10,000.00 / (100,000.00 + 0.5 * 10,000.00) = 9.52% |
| January 3, 2023 | 20,000.00 | 3,000.00 | 123,000.00 | |
| January 4, 2023 | -- | 1,000.00 | 124,000.00 | |
| January 5, 2023 | -10,000.00 | 5,000.00 | 119,000.00 | |
| January 6, 2023 (end of the period) | -- | 1,000.00 | 120,000.00 | |
| Total | 10,000.00 | 10,000.00 |
Examples are provided for illustrative purposes only and not intended to be reflective of results any investor can expect to achieve.
2.2 Money-Weighted Return Method
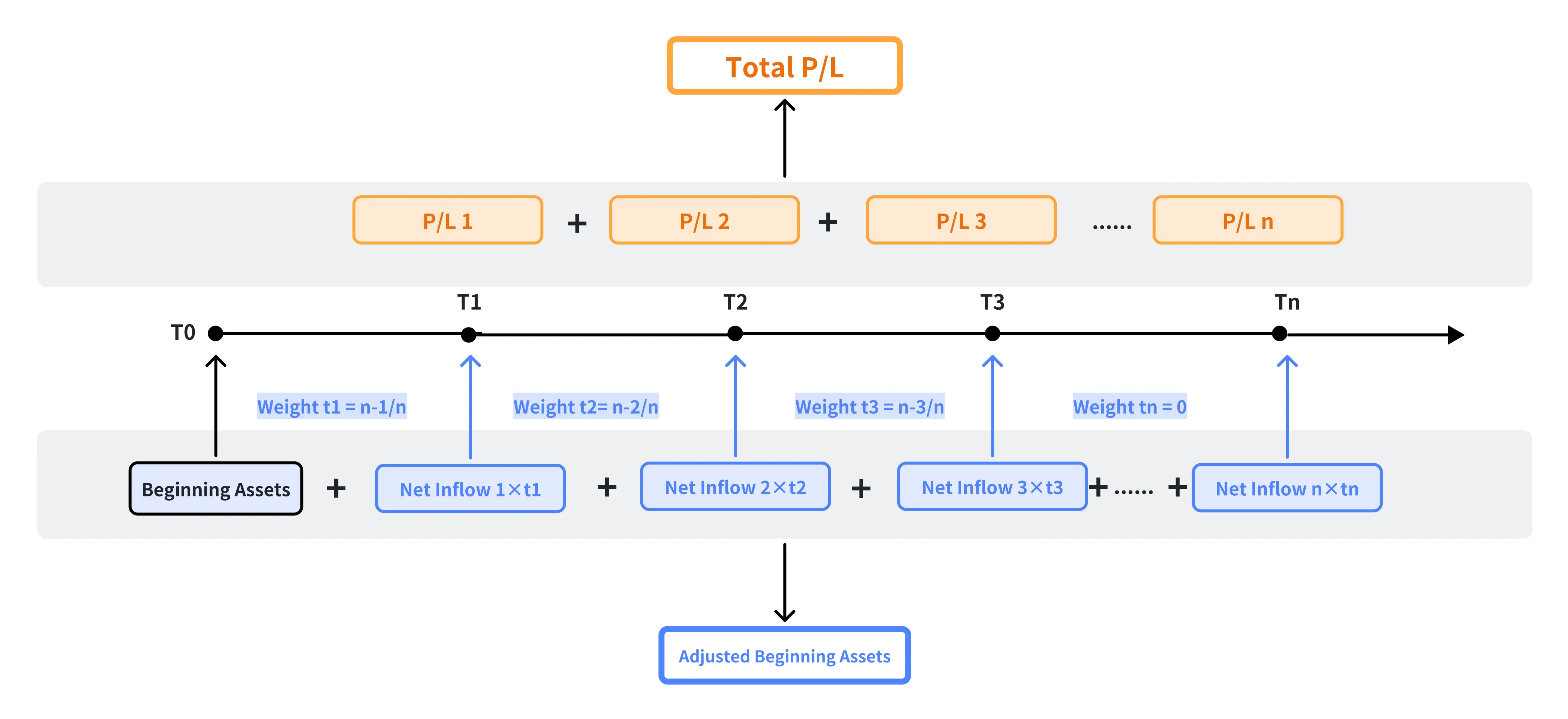
This method calculates the impact of net inflows by using their weights, i.e. the length of time that each net inflow was maintained during the measurement period, and thus gets the adjusted beginning assets. It considers the timing and size of the net inflows and generally gives a more accurate result than the simple Dietz method does when there are frequent deposits and withdrawals.
Formula: Total Rate of Return = Total P/L / Adjusted Beginning Assets
Where:
(1) Adjusted Beginning Assets = Beginning Assets + ∑ (Net Inflow * Weight)
(2) Weight = Time of Net Inflow / Total Number of Days
Example:
| Date | Net Inflow | Daily P/L | Total Assets | Time of Net Inflow | Weight | Net Inflow * Weight | Calculation |
| January 2, 2023 (beginning of the period) | -- | -- | 100,000.00 | 4 days | -- | -- | Total Rate of Return = 10,000.00 / (100,000.00 + 12,500.00) = 8.89% |
| January 3, 2023 | 20,000.00 | 3,000.00 | 123,000.00 | 3 days | 0.75 | 15,000.00 | |
| January 4, 2023 | -- | 1,000.00 | 124,000.00 | 2 days | 0.5 | 0.00 | |
| January 5, 2023 | -10,000.00 | 5,000.00 | 119,000.00 | 1 day | 0.25 | -2,500.00 | |
| January 6, 2023 (end of the period) | -- | 1,000.00 | 120,000.00 | 0 days | 0 | 0.00 | |
| Total | 10,000.00 | 10,000.00 | 12,500.00 |
Examples are provided for illustrative purposes only and not intended to be reflective of results any investor can expect to achieve.
2.3 Time-Weighted Return Method
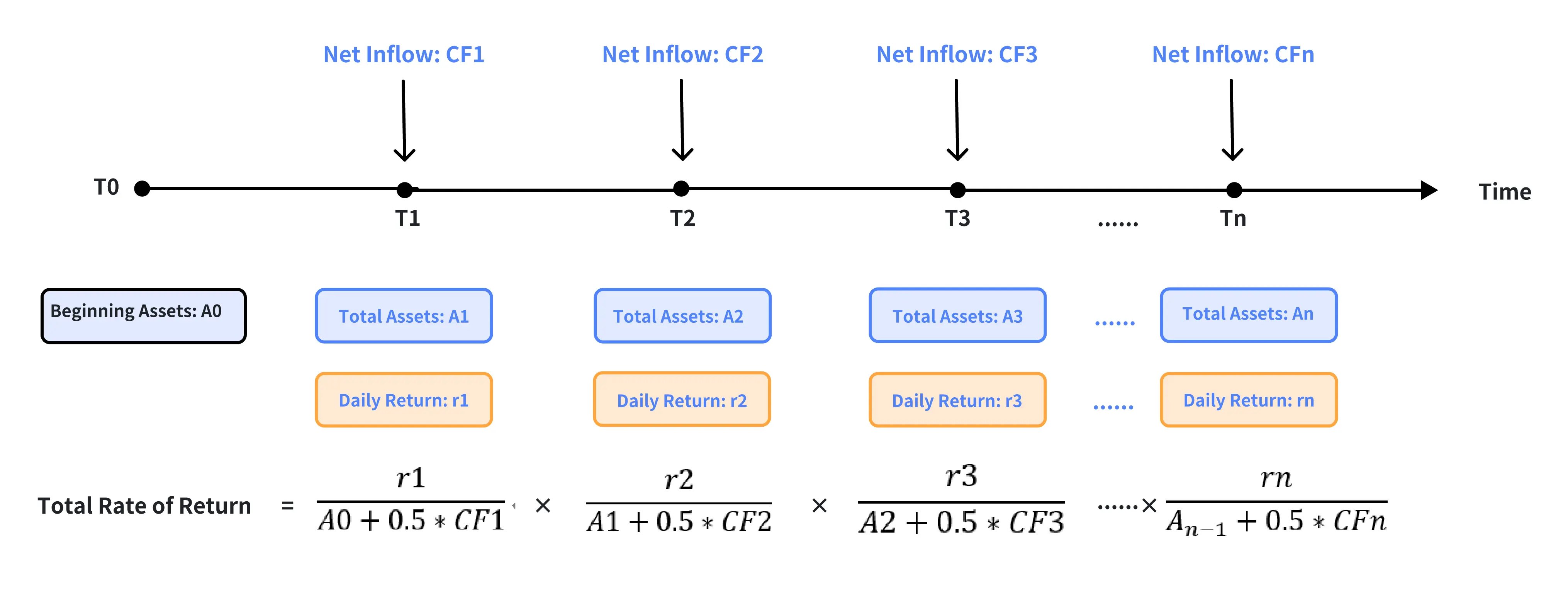
By dividing the entire measurement period by day, this method first calculates the rate of return for each day and then geometrically links them to obtain the total rate of return.
It divides net inflows by day and generally gives a more accurate result than the simple Dietz method does when there are frequent deposits and withdrawals. However, large deposits and withdrawals may lead to a rate of return with an opposite sign to the cumulative P/L, which should be considered meaningless (see 3.4 for details).
Formula: Total Rate of Return = [(1 + R1) * (1 + R2) * (1 + R3) … (1 + Rn) - 1] * 100%
Example:
| Date | Net Inflow | Daily P/L | Total Assets | Daily Rate of Return | Calculation |
| January 2, 2023 (beginning of the period) | -- | -- | 100,000.00 | -- | Total Rate of Return = (1 + 2.73%) * (1 + 0.81%) * ( 1+ 4.20%) * (1 + 0.84%) - 1 = 8.82% |
| January 3, 2023 | 20,000.00 | 3,000.00 | 123,000.00 | 2.73% | |
| January 4, 2023 | -- | 1,000.00 | 124,000.00 | 0.81% | |
| January 5, 2023 | -10,000.00 | 5,000.00 | 119,000.00 | 4.20% | |
| January 6, 2023 (end of the period) | -- | 1,000.00 | 120,000.00 | 0.84% | |
| Total | 10,000.00 | 10,000.00 |
Examples are provided for illustrative purposes only and not intended to be reflective of results any investor can expect to achieve.
3. FAQ
3.1 What are the differences between these calculation methods?
As is shown in Section 2 (Calculation Methods for Rate of Return), the three calculation methods give different results under the same condition. They have different application scenarios, as well as different advantages and disadvantages. You can choose among these methods as you wish according to the scenarios and your own needs.
| Method | Formula/Description | Application Scenario | Advantage | Disadvantage |
| Simple Dietz Method | Total P/L / Adjusted Beginning Assets It calculates the impact of all net inflows by using a coefficient of 0.5 and thus gets the adjusted beginning assets. |
Less frequent or smaller deposits and withdrawals | Easy to understand | Compared with the other two methods, it gives a relatively inaccurate result. In particular, if you transfer many funds out, or if the measurement period is long, it may distort and exaggerate the rate of return, or even give a negative number without any meaning. |
| Money-Weighted Return Method | Total P/L / Adjusted Beginning Assets It calculates the impact of net inflows by using their weights, i.e. the length of time that each net inflow was maintained during the measurement period, and then gets the adjusted beginning assets. |
Frequent deposits and withdrawals | It considers the timing and size of net inflows. Compared with the time-weighted return method, there is a lower probability that the resulting rate of return has an opposite sign to the P/L. | If you make frequent, large transfers during the measurement period and the measurement period is long, you may not get an accurate total rate of return. |
| Time-Weighted Return Method | It first calculates the rate of return for each day during the measurement period and then geometrically link them to get the total rate of return | It divides the measurement period by day, thus minimizing the impact of net inflows on the rate of return | It does not consider the amount of investment and treats all daily rates of return equally. If you make frequent, large deposits and withdrawals (relative to the net assets in your account), you may get a rate of return with an opposite sign to your P/L and thus becomes meaningless. |
3.2 Why do these calculation methods give different results?
As mentioned in Table 3.1 above, since both the measurement period and the net inflows during the measurement period are treated in different ways under these methods, they give different results.
3.3 How do I choose among these calculation methods?
If your account has no net inflow during the measurement period, all three methods will give the same and accurate rate of return; however, if there are net inflows during the period, you may get different results. The longer the period, the greater the difference.
For most investors, we suggest that they consider using the time-weighted return method first, then the money-weighted return method, and then the simple Dietz method.
3.4 Why does my return have an opposite sign to my cumulative P/L?
Since all calculation methods consider the “total assets" factor, if you make frequent, large deposits and withdrawals and your total assets decrease, your cumulative P/L may have an opposite sign to your rate of return. It is usually the case when you use the time-weighted return method. For example, since Daily P/L / (Previous Total Assets + 0.5 * Daily Net Inflow):
(1) For Day T: Your total assets start at 100 and end at 150 with no net inflows. This results in a daily P/L of +50 and a daily rate of return of +50.00%.
(2) For Day T+1: Your total assets start at 150 and end at 1,050, with a net inflow of 1,000. This leads to a daily P/L of –100 and a daily rate of return of –15.38%.
(3) For Days T to T+1: Your rate of return under the TWR method is [(1+ 50.00%) * (1 – 15.38%) – 1] * 100% = +26.93%, but your cumulative P/L is 50 – 100 = –50.
In this case, your rate of return does not accurately reflect the actual P/L for the positions, so please refer to your cumulative P/L or switch to the other two methods. If you still get a rate of return with an opposite sign to your cumulative P/L after using either of the other two methods, please contact our customer service for help.
This content is for informational and educational use only and is not a recommendation or endorsement of any particular investment or investment strategy. Investment information provided in this content is general in nature, strictly for illustrative purposes, and may not be appropriate for all investors. It is provided without respect to individual investors’ financial sophistication, financial situation, investment objectives, investing time horizon, or risk tolerance. You should consider the appropriateness of this information having regard to your relevant personal circumstances before making any investment decisions. Past investment performance does not indicate or guarantee future success. Returns will vary, and all investments carry risks, including loss of principal. FUTU HK makes no representation or warranty as to its adequacy, completeness, accuracy or timeliness for any particular purpose of the above content.